One of my hobbies is sacred geometry - loosely defined, it’s the study and use of mathematical archetypes in nature and culture, often with a focus on traditional compass and straightedge constructions.
Don’t worry; I’m not about to go off into numerology, telling you that you can derive the groovy cosmic secrets of the ancients by studying numeric coincidences. I actually take a rather dim reading spurious meaning into special cases of the Interesting Number Theorem.* The worst case scenario might resemble the Arronofsky film “Pi”, except without the sweet soundtrack.
Nonetheless, exploring the traditions behind sacred geometry can give insight into art and design. The traditional compass and straightedge drove the development of mathematics until just a century or two ago, and modern algebra has its roots in questions about why it is, exactly, that you can’t construct a perfect heptagon. The practice is also fun and relaxing, and can even give occasional insights into physical reality.
One subject that comes up a lot in these discussions is a number called the golden ratio, sometimes abbreviated phi. Phi is defined in terms of the relationship between a line segment and its parts.
Imagine that you draw a line segment, and then you choose a very special point on it. This point divides the segment into two new pieces, a small one and a big one. The point you’ve chosen is special because the ratio of the small piece to the large piece is the same as the large piece to the whole thing. This ratio is phi.
One thing that I think is really cool about phi is that it’s hopelessly self-referential. Self-reference when a system ‘talks about’ itself in some way or another. This sentence, for example, is self-referential. So is this one. (Self-reference leads to all sorts of fun system-level properties like Russel’s Paradox; if you’d like to know more, you might want to check out Douglas Hofstader’s book, Godel Escher Bach: An Eternal Golden Braid.) (Hofstader 1979)
My favorite example comes from remembering that phi is the solution of a quadratic equation, which can be rearranged to express phi as a fraction. However, the fraction itself contains phi, which means that you can use the equation to put the fraction… inside of the fraction! Phi is also the limit of the ratio of successive terms of the Fibonacci sequence, which are defined by reference to earlier terms. Self-reference again!
This sort of recursive structure, in which a structure is composed of smaller copies of itself, is a common theme in fractals like the Menger sponge.
Phi is also intimately connected to the pentagram. For example, if you look at the arm of a pentagram, it’s broken into two pieces, one smaller, one bigger. The ratio of the larger to the smaller is the same as the ratio of the whole to the larger - and that ratio is phi. Pentagrams are also self-referential; every pentagram contains a pentagon, and thus another pentagram. It contains a factory for making more of itself.
If you look at bathroom tiles or an Escher print, you’ll see a lot of rectangles, some hexagons, maybe a few triangles repeating over and over. Imagine picking up the pattern and sliding it around on the bathroom floor: if you only slide it, not twisting or flipping, you’ll be able to line the pattern back up with the tiles. This is called translational symmetry. You won’t see many pentagons, though, because as it happens, you can’t tile the plane with regular, repeating pentagonal shapes. In order to tile a plane with pentagons, you have to give up the requirement of translational symmetry. Then, you get things like the Penrose tiling, which creates self-similar (and thus self-referential) “quasicrystals”, so called because they lack the repetitive translational symmetry of crystals.
If you’ve ever grown crystals, you might have used a seed crystal, a small crystal you drop into the solution giving growing crystals a lattice on which to form. But what if you use a quasicrystal, without a regular lattice, as the seed? Researchers investigated this question at the European Syncrotron Radiation Facility by making a pentagonally tiled silicon surface, and growing gold/silicon crystals on it. They found that the pentagonal substrate allowed the gold/silicon mixture to stay liquid far below its typical melting point, a phenomenon called supercooling. Apparently, the pentagonal substrate induces unpackable icosahedral structures inside the liquid; because they can’t pack into regular crystals, these structures don’t readily solidify. (Schulli et al 2010)
That’s an exotic, somewhat contrived example, but the same principles are proposed as an explanation for how droplets of water can remain liquid in high-altitude clouds. For a long time the only known quasicrystals were artificially prepared materials like the gold/silicon mixture. That changed last year, as researchers reported the discovery of a natural quasicrystal, embedded in what appears to be a meteorite. This sample was quite old, probably around 4.5 billion years, suggesting that quasicrystals can be very stable structures. (Bindi et al 2012).
This revelation really makes me curious. If a pentagonal substrate can induce structures in a liquid, which can resist crystallization at sub-freezing temperatures, then what else might they be capable of? Surface layer effects are important in many sorts of catalysis, so perhaps there are interesting reactions which could be catalyzed by aperiodic substrates. There is a long tradition of comparing life’s organic structure to aperiodic quasicrystals, from Schrodinger’s What is Life? to the Cairns-Smith hypothesis of abiogenesis. (Hofstader 1979) It would certainly be interesting if quasicrystals like that found in an ancient meteorite played a role in early biochemistry. I also like to ponder the observation that some viruses like tobacco mosaic virus can be crystallized, being shaped like packable rods, while other,s such as the herpes virus, are shaped like unpackable icosahedra. Is packability important to some viral niches but not others?
~~~
*Theorem: All natural numbers are interesting.
Proof: Proceed by induction. Consider zero – a number so interesting that the medieval church banned it. Next, there’s one – the only number that’s neither prime nor composite, the identity element of multiplication, and the generator element for addition. Then, there’s two – the only even prime. After that, there’s three, the smallest possible number of sides you can have in a polygon. I could continue, but we’ve already established the basis step.
Now, assume that every number up to N is interesting, and consider the number N+1. This would be the first boring number - and that would be pretty interesting! (QED and/or LULZ)
Luca Bindi, John M. Eiler, Yunbin Guan, Lincoln S. Hollister, Glenn MacPherson, Paul J. Steinhardt, & Nan Yao (2012). Evidence for the extraterrestrial origin of a natural quasicrystal Proceedings of the National Academy of Sciences of the United States of America, 109 (5), 1396-1401 DOI: 10.1073/pnas.1111115109
Schülli TU, Daudin R, Renaud G, Vaysset A, Geaymond O, & Pasturel A (2010). Substrate-enhanced supercooling in AuSi eutectic droplets. Nature, 464 (7292), 1174-7 PMID: 20414305



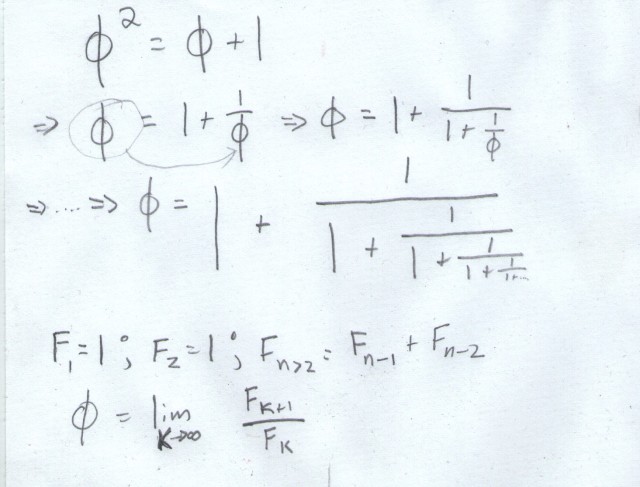




Love this one! And right at the beginning, about the heptagon: I used to have a set of drinking glasses that had 7 bevelled sides. I always loved them because I found that so odd. Wonder who created that mold? and how? Unfortunately, they all were broken. Thanks, Chuck! See you tomorrow night!
:3